本文摘自php中文网,作者不言,侵删。
这篇文章主要介绍了关于用TensorFlow实现戴明回归算法的示例,有着一定的参考价值,现在分享给大家,有需要的朋友可以参考一下如果最小二乘线性回归算法最小化到回归直线的竖直距离(即,平行于y轴方向),则戴明回归最小化到回归直线的总距离(即,垂直于回归直线)。其最小化x值和y值两个方向的误差,具体的对比图如下图。
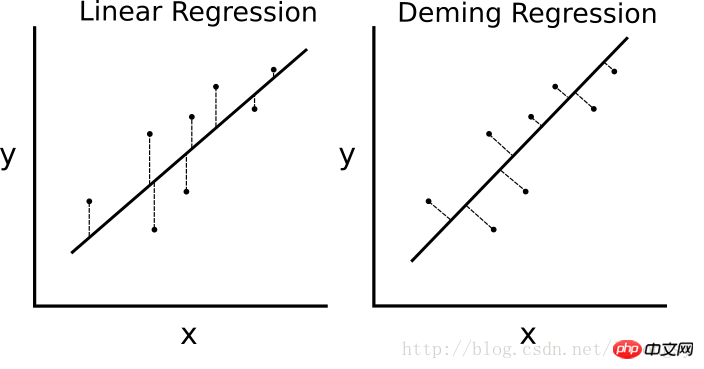
线性回归算法和戴明回归算法的区别。左边的线性回归最小化到回归直线的竖直距离;右边的戴明回归最小化到回归直线的总距离。
线性回归算法的损失函数最小化竖直距离;而这里需要最小化总距离。给定直线的斜率和截距,则求解一个点到直线的垂直距离有已知的几何公式。代入几何公式并使TensorFlow最小化距离。
损失函数是由分子和分母组成的几何公式。给定直线y=mx+b,点(x0,y0),则求两者间的距离的公式为:
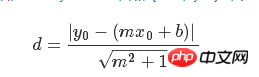
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 |
|
结果:
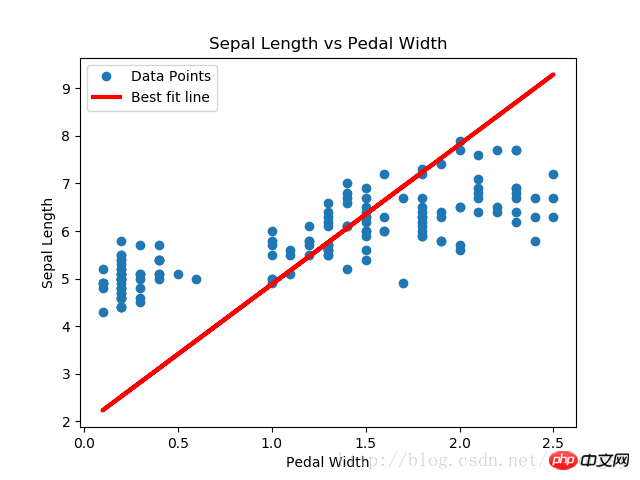
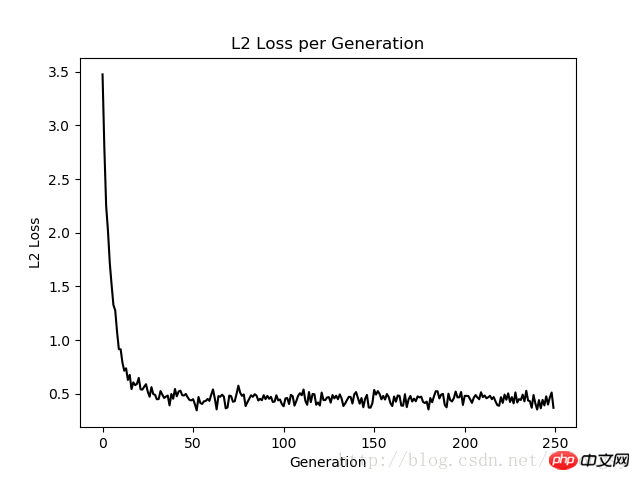
本文的戴明回归算法与线性回归算法得到的结果基本一致。两者之间的关键不同点在于预测值与数据点间的损失函数度量:线性回归算法的损失函数是竖直距离损失;而戴明回归算法是垂直距离损失(到x轴和y轴的总距离损失)。
注意,这里戴明回归算法的实现类型是总体回归(总的最小二乘法误差)。总体回归算法是假设x值和y值的误差是相似的。我们也可以根据不同的理念使用不同的误差来扩展x轴和y轴的距离计算。
相关推荐:
用TensorFlow实现多类支持向量机的示例代码
TensorFlow实现非线性支持向量机的实现方法
以上就是用TensorFlow实现戴明回归算法的示例的详细内容,更多文章请关注木庄网络博客!!
相关阅读 >>
更多相关阅读请进入《Python》频道 >>

Python编程 从入门到实践 第2版
python入门书籍,非常畅销,超高好评,python官方公认好书。




