本文摘自php中文网，作者零到壹度，侵删。
本文实例讲述了Python实现LR经典算法。分享给大家供大家参考，具体如下：（一）认识Logistic回归（LR）分类器
首先，Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题，利用Logistic函数（或称为Sigmoid函数），自变量取值范围为(-INF, INF)，自变量的取值范围为(0,1)，函数形式为：
由于sigmoid函数的定义域是(-INF, +INF),而值域为(0, 1)。因此最基本的LR分类器适合于对两分类（类0，类1）目标进行分类。Sigmoid 函数是个很漂亮的“S”形，如下图所示：
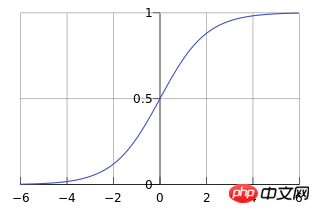
LR分类器(Logistic Regression Classifier)目的就是从训练数据特征学习出一个0/1分类模型--这个模型以样本特征的线性组合
作为自变量，使用logistic函数将自变量映射到(0,1)上。因此LR分类器的求解就是求解一组权值
（
是是名义变量--dummy，为常数，实际工程中常另x0=1.0。不管常数项有没有意义，最好保留），并代入Logistic函数构造出一个预测函数：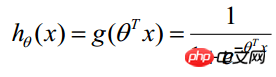
函数的值表示结果为1的概率，就是特征属于y=1的概率。因此对于输入x分类结果为类别1和类别0的概率分别为：
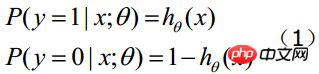
当我们要判别一个新来的特征属于哪个类时，按照下式求出一个z值：
（x1,x2,...,xn是某样本数据的各个特征，维度为n）
进而求出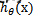
---若大于0.5就是y=1的类，反之属于y=0类。（注意：这里依然假设统计样本是均匀分布的，所以设阈值为0.5）。LR分类器的这一组权值如何求得的呢？这就需要涉及到极大似然估计MLE和优化算法的概念了，数学中最优化算法常用的就是梯度上升（下降）算法。
Logistic回归可以也可以用于多分类的，但是二分类的更为常用也更容易解释。所以实际中最常用的就是二分类的Logistic回归。LR分类器适用数据类型：数值型和标称型数据。其优点是计算代价不高，易于理解和实现；其缺点是容易欠拟合，分类精度可能不高。
（二）Logistic回归数学推导
1，梯度下降法求解Logistic回归
首先，理解下述数学推导过程需要较多的导数求解公式，可以参考“常用基本初等函数求导公式积分公式”。
假设有n个观测样本，观测值分别为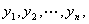
设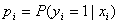
为给定条件下得到yi=1的概率。在同样条件下得到yi=0的条件概率为
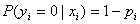。于是，得到一个观测值的概率为
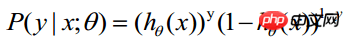-----此公式实际上是综合公式（1）得出
因为各项观测独立，所以它们的联合分布可以表示为各边际分布的乘积：
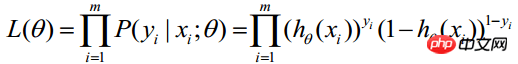（m表统计样本数目）
上式称为n个观测的似然函数。我们的目标是能够求出使这一似然函数的值最大的参数估计。于是，最大似然估计的关键就是求出参数，使上式取得最大值。
对上述函数求对数：
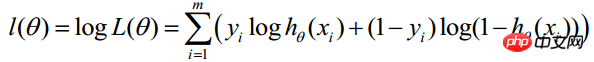
最大似然估计就是求使上式取最大值时的θ，这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。在Andrew Ng的课程中将J(θ)取为下式，即：J(θ)=-(1/m)l(θ)，J(θ)最小值时的θ则为要求的最佳参数。通过梯度下降法求最小值。θ的初始值可以全部为1.0，更新过程为：
（j表样本第j个属性，共n个；a表示步长--每次移动量大小，可自由指定）
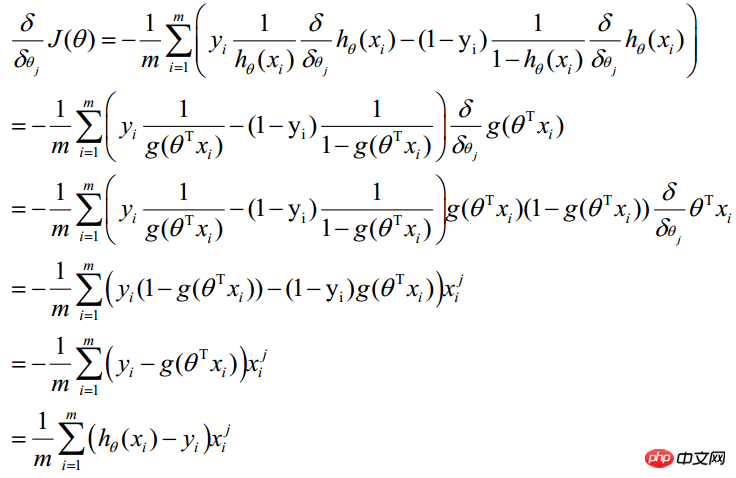
因此，θ（可以设初始值全部为1.0）的更新过程可以写成：
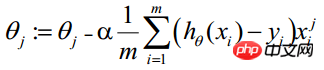（i表示第i个统计样本，j表样本第j个属性；a表示步长）
该公式将一直被迭代执行，直至达到收敛（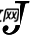
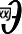
在每一步迭代中都减小，如果某一步减少的值少于某个很小的值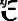
（小于0.001）, 则其判定收敛）或某个停止条件为止（比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围）。
2，向量化Vectorization求解
Vectorization是使用矩阵计算来代替for循环，以简化计算过程，提高效率。如上式，Σ(...)是一个求和的过程，显然需要一个for语句循环m次，所以根本没有完全的实现vectorization。下面介绍向量化的过程：
约定训练数据的矩阵形式如下，x的每一行为一条训练样本，而每一列为不同的特称取值：
相关阅读 >>
Python脚本生成caffe train_list.txt的方法
更多相关阅读请进入《Python》频道 >>
Python编程 从入门到实践 第2版
python入门书籍，非常畅销，超高好评，python官方公认好书。
