本文摘自php中文网,作者黄舟,侵删。
这篇文章主要给大家介绍了关于利用python如何求解物理学中的双弹簧质能系统的相关资料,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧。前言
本文主要给大家介绍了关于利用python求解物理学中双弹簧质能系统的相关内容,分享出来供大家参考学习,下面话不多说了,来一起看看详细的介绍吧。
物理的模型如下:
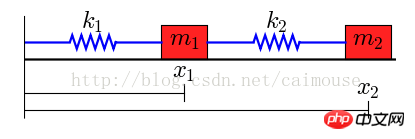
在这个系统里有两个物体,它们的质量分别是m1和m2,被两个弹簧连接在一起,伸缩系统为k1和k2,左端固定。假定没有外力时,两个弹簧的长度为L1和L2。
由于两物体有重力,那么在平面上形成摩擦力,那么摩擦系数分别为b1和b2。所以可以把微分方程写成这样:
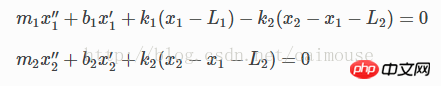
这是一个二阶的微分方程,为了使用python来求解,需要把它转换为一阶微分方程。所以引入下面两个变量:

这两个相当于运动的速度。通过运算可以改为这样:
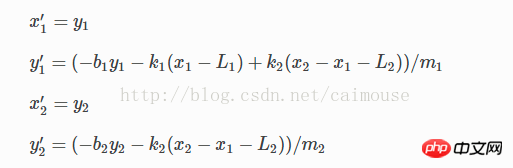
这时可以线性方程改为向量数组的方式,就可以使用python定义了
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
|
在这里把结果输出到文件two_springs.dat,接着写一个程序来把数据显示成图片,就可以发表论文了,代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
|
最后来查看一下输出的png图片如下:
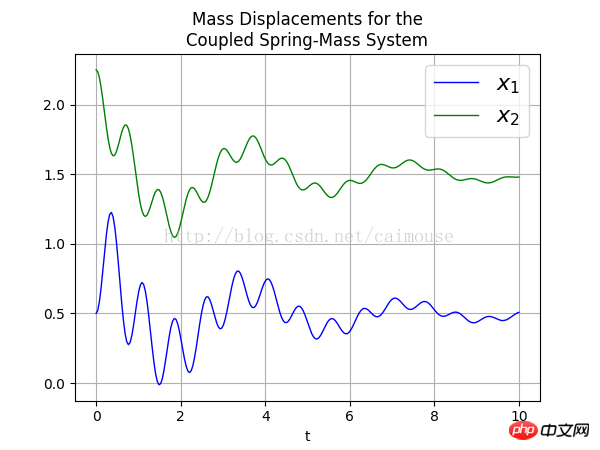
总结
以上就是python求解物理学中的双弹簧质能系统的代码实例的详细内容,更多文章请关注木庄网络博客!!
相关阅读 >>
对Python中dataframe按照行遍历的方法_Python
Python通过属性手段实现只允许调用一次的示例讲解_Python
更多相关阅读请进入《Python》频道 >>

Python编程 从入门到实践 第2版
python入门书籍,非常畅销,超高好评,python官方公认好书。




