本文摘自php中文网,作者巴扎黑,侵删。
这篇文章主要介绍了Python基于回溯法子集树模板实现8皇后问题,简单说明了8皇后问题的原理并结合实例形式分析了Python回溯法子集树模板解决8皇后问题的具体实现技巧,需要的朋友可以参考下本文实例讲述了Python基于回溯法子集树模板实现8皇后问题。分享给大家供大家参考,具体如下:
问题
8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。

分析
为了简化问题,考虑到8个皇后不同行,则每一行放置一个皇后,每一行的皇后可以放置于第0、1、2、...、7列,我们认为每一行的皇后有8种状态。那么,我们只要套用子集树模板,从第0行开始,自上而下,对每一行的皇后,遍历它的8个状态即可。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
效果图
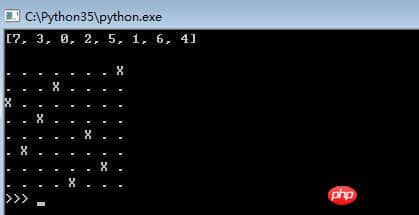
以上就是解决Python基于回溯法子集树模板实现8皇后问题的详细内容,更多文章请关注木庄网络博客!!
相关阅读 >>
详解Python利用flask sqlalchemy实现分页
更多相关阅读请进入《Python》频道 >>

Python编程 从入门到实践 第2版
python入门书籍,非常畅销,超高好评,python官方公认好书。




