CPU 和 内存就像是一堆不可分割的恋人一样,是无法拆散的一对儿,没有内存,CPU 无法执行程序指令,那么计算机也就失去了意义;只有内存,无法执行指令,那么计算机照样无法运行。
那么什么是内存?内存和 CPU 如何进行交互?下面就来介绍一下
什么是内存
内存(Memory)是计算机中最重要的部件之一,它是程序与CPU进行沟通的桥梁。
计算机中所有程序的运行都是在内存中进行的,因此内存对计算机的影响非常大,内存又被称为主存,其作用是存放 CPU 中的运算数据,以及与硬盘等外部存储设备交换的数据。
只要计算机在运行中,CPU 就会把需要运算的数据调到主存中进行运算,当运算完成后CPU再将结果传送出来,主存的运行也决定了计算机的稳定运行。
内存的物理结构
内存的内部是由各种 IC 电路组成的,它的种类很庞大,但是其主要分为三种存储器
随机存储器(RAM): 内存中最重要的一种,表示既可以从中读取数据,也可以写入数据。当机器关闭时,内存中的信息会丢失。
只读存储器(ROM):ROM 一般只能用于数据的读取,不能写入数据,但是当机器停电时,这些数据不会丢失。
高速缓存(Cache):Cache 也是我们经常见到的,它分为一级缓存(L1 Cache)、二级缓存(L2 Cache)、三级缓存(L3 Cache)这些数据,它位于内存和 CPU 之间,是一个读写速度比内存更快的存储器。当 CPU 向内存写入数据时,这些数据也会被写入高速缓存中。当 CPU 需要读取数据时,会直接从高速缓存中直接读取,当然,如需要的数据在Cache中没有,CPU会再去读取内存中的数据。
内存 IC 是一个完整的结构,它内部也有电源、地址信号、数据信号、控制信号和用于寻址的 IC 引脚来进行数据的读写。
下面是一个虚拟的 IC 引脚示意图
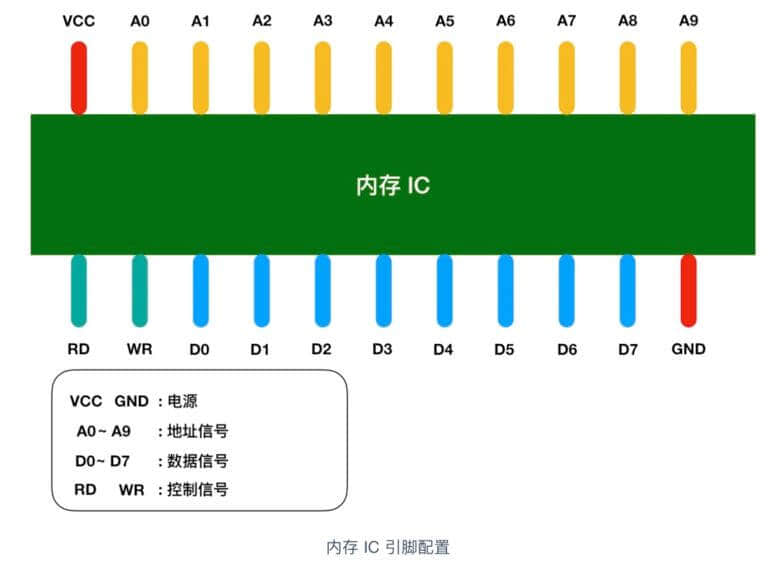
图中 VCC 和 GND 表示电源,A0 - A9 是地址信号的引脚,D0 - D7 表示的是控制信号、RD 和 WR 都是好控制信号,我用不同的颜色进行了区分,将电源连接到 VCC 和 GND 后,就可以对其他引脚传递 0 和 1 的信号,大多数情况下,+5V 表示1,0V 表示 0。
我们都知道内存是用来存储数据,那么这个内存 IC 中能存储多少数据呢?
D0 - D7 表示的是数据信号,也就是说,一次可以输入输出 8 bit = 1 byte 的数据。
A0 - A9 是地址信号共十个,表示可以指定 00000 00000 - 11111 11111 共 2 的 10次方 = 1024个地址。
每个地址都会存放 1 byte 的数据,因此我们可以得出内存 IC 的容量就是 1 KB。
内存的读写过程
让我们把关注点放在内存 IC 对数据的读写过程上来吧!
我们来看一个对内存IC 进行数据写入和读取的模型
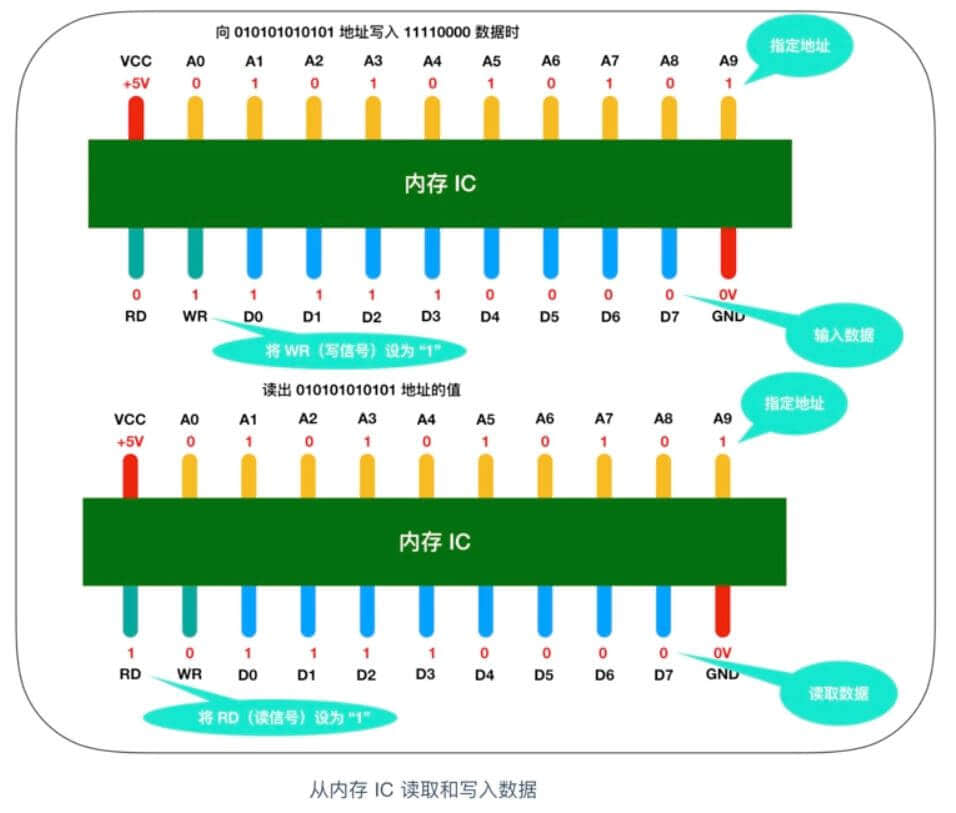
来详细描述一下这个过程,假设我们要向内存 IC 中写入 1byte 的数据的话,它的过程是这样的:首先给 VCC 接通 +5V 的电源,给 GND 接通 0V 的电源,使用 A0 - A9 来指定数据的存储场所,然后再把数据的值输入给 D0 - D7 的数据信号,并把 WR(write)的值置为 1,执行完这些操作后,即可以向内存 IC 写入数据读出数据时,只需要通过 A0 - A9 的地址信号指定数据的存储场所,然后再将 RD 的值置为 1 即可。
图中的 RD 和 WR 又被称为控制信号。
其中当WR 和 RD 都为 0 时,无法进行写入和读取操作。
内存的现实模型
为了便于记忆,我们把内存模型映射成为我们现实世界的模型,在现实世界中,内存的模型很想我们生活的楼房。
在这个楼房中,1层可以存储一个字节的数据,楼层号就是地址,下面是内存和楼层整合的模型图
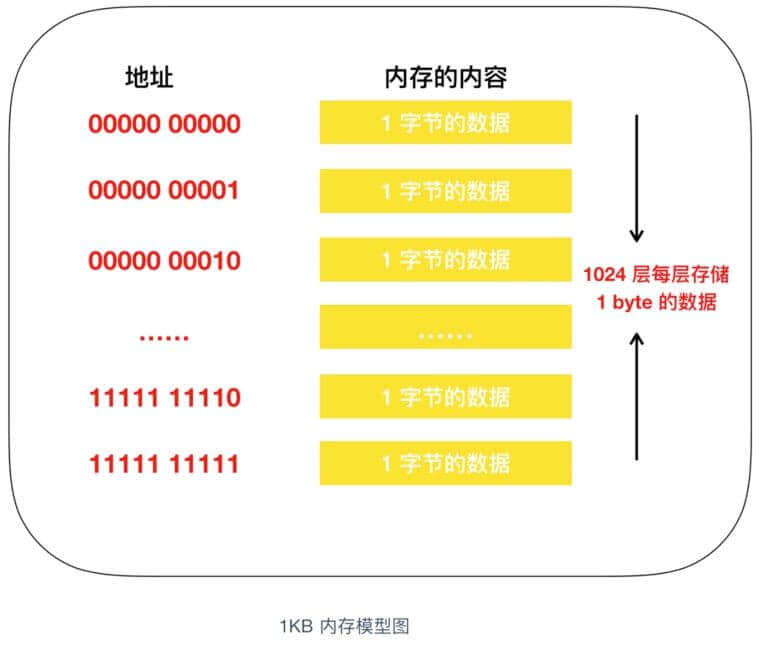
我们知道,程序中的数据不仅只有数值,还有数据类型的概念,从内存上来看,就是占用内存大小(占用楼层数)的意思。
即使物理上强制以 1 个字节为单位来逐一读写数据的内存,在程序中,通过指定其数据类型,也能实现以特定字节数为单位来进行读写。
二进制
我们都知道,计算机的底层都是使用二进制数据进行数据流传输的,那么为什么会使用二进制表示计算机呢?
或者说,什么是二进制数呢?
在拓展一步,如何使用二进制进行加减乘除?
下面就来看一下
什么是二进制数
那么什么是二进制数呢?
为了说明这个问题,我们先把 00100111 这个数转换为十进制数看一下,二进制数转换为十进制数,直接将各位置上的值 * 位权即可,那么我们将上面的数值进行转换

也就是说,二进制数代表的 00100111 转换成十进制就是 39,这个 39 并不是 3 和 9 两个数字连着写,而是 3 * 10 + 9 * 1,这里面的 10 , 1 就是位权,以此类推,上述例子中的位权从高位到低位依次就是 7 6 5 4 3 2 1 0。
这个位权也叫做次幂,那么最高位就是2的7次幂,2的6次幂 等等。
二进制数的运算每次都会以2为底,这个2 指得就是基数,那么十进制数的基数也就是 10 。
在任何情况下位权的值都是 数的位数 - 1,那么第一位的位权就是 1 - 1 = 0, 第二位的位权就睡 2 - 1 = 1,以此类推。
那么我们所说的二进制数其实就是 用0和1两个数字来表示的数,它的基数为2,它的数值就是每个数的位数 * 位权再求和得到的结果,我们一般来说数值指的就是十进制数,那么它的数值就是 3 * 10 + 9 * 1 = 39。
移位运算和乘除的关系
在了解过二进制之后,下面我们来看一下二进制的运算,和十进制数一样,加减乘除也适用于二进制数,只要注意逢 2 进位即可。
二进制数的运算,也是计算机程序所特有的运算,因此了解二进制的运算是必须要掌握的。
首先我们来介绍移位 运算,移位运算是指将二进制的数值的各个位置上的元素坐左移和右移操作,见下图

补数
刚才我们没有介绍右移的情况,是因为右移之后空出来的高位数值,有 0 和 1 两种形式。
要想区分什么时候补0什么时候补1,首先就需要掌握二进制数表示负数的方法。
二进制数中表示负数值时,一般会把最高位作为符号来使用,因此我们把这个最高位当作符号位。
符号位是 0 时表示正数,是 1 时表示 负数。
那么 -1 用二进制数该如何表示呢?
可能很多人会这么认为: 因为 1 的二进制数是 0000 0001,最高位是符号位,所以正确的表示 -1 应该是 1000 0001,但是这个答案真的对吗?
计算机世界中是没有减法的,计算机在做减法的时候其实就是在做加法,也就是用加法来实现的减法运算。
比如 100 - 50 ,其实计算机来看的时候应该是 100 + (-50),为此,在表示负数的时候就要用到二进制补数,补数就是用正数来表示的负数。
为了获得补数,我们需要将二进制的各数位的数值全部取反,然后再将结果 + 1 即可,先记住这个结论,下面我们来演示一下。

具体来说,就是需要先获取某个数值的二进制数,然后对二进制数的每一位做取反操作(0 ---> 1 , 1 ---> 0),最后再对取反后的数 +1 ,这样就完成了补数的获取。
补数的获取,虽然直观上不易理解,但是逻辑上却非常严谨,比如我们来看一下 1 - 1 的这个过程,我们先用上面的这个 1000 0001(它是1的补数,不知道的请看上文,正确性先不管,只是用来做一下计算)来表示一下
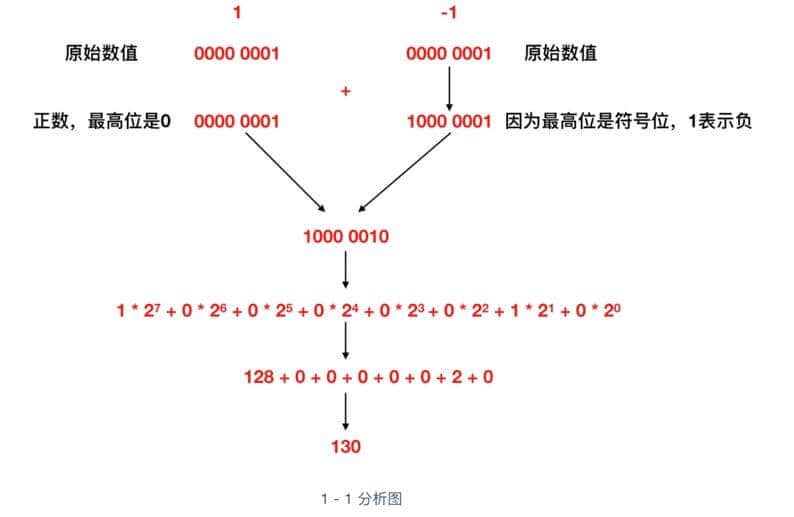
奇怪,1 - 1 会变成 130 ,而不是0,所以可以得出结论 1000 0001 表示 -1 是完全错误的。
那么正确的该如何表示呢?
其实我们上面已经给出结果了,那就是 1111 1111,来论证一下它的正确性
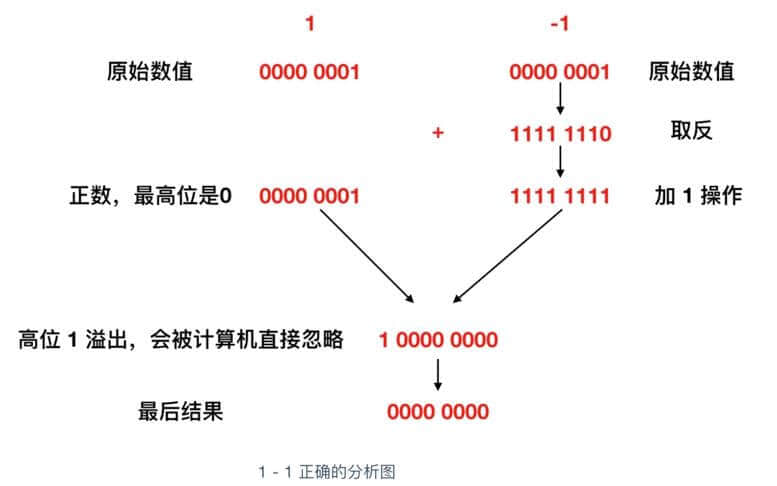
我们可以看到 1 - 1 其实实际上就是 1 + (-1),对 -1 进行上面的取反 + 1 后变为 1111 1111, 然后与 1 进行加法运算,得到的结果是九位的 1 0000 0000,结果发生了溢出,计算机会直接忽略掉溢出位,也就是直接抛掉 最高位 1 ,变为 0000 0000。
也就是 0,结果正确,所以 1111 1111 表示的就是 -1 。
所以负数的二进制表示就是先求其补数,补数的求解过程就是对原始数值的二进制数各位取反,然后将结果 + 1。
算数右移和逻辑右移的区别
在了解完补数后,我们重新考虑一下右移这个议题,右移在移位后空出来的最高位有两种情况 0 和 1。
将二进制数作为带符号的数值进行右移运算时,移位后需要在最高位填充移位前符号位的值( 0 或 1)。
这就被称为算数右移。
如果数值使用补数表示的负数值,那么右移后在空出来的最高位补 1,就可以正确的表示 1/2,1/4,1/8等的数值运算。
如果是正数,那么直接在空出来的位置补 0 即可。
下面来看一个右移的例子。
将 -4 右移两位,来各自看一下移位示意图
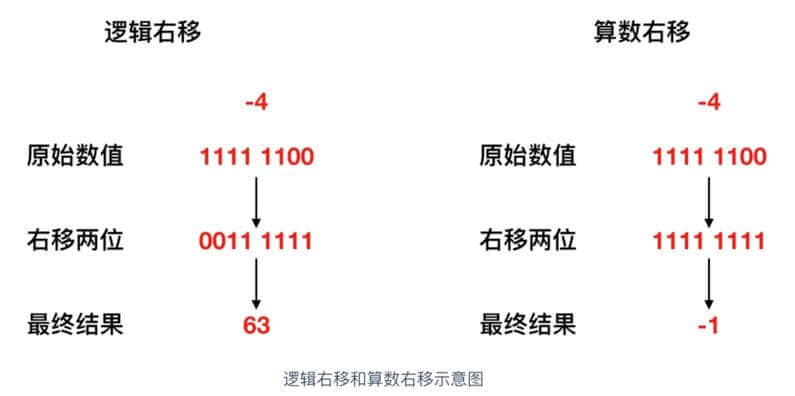
如上图所示,在逻辑右移的情况下, -4 右移两位会变成 63, 显然不是它的 1/4,所以不能使用逻辑右移,那么算数右移的情况下,右移两位会变为 -1,显然是它的 1/4,故而采用算数右移。
那么我们可以得出来一个结论:左移时,无论是图形还是数值,移位后,只需要将低位补 0 即可;右移时,需要根据情况判断是逻辑右移还是算数右移。
下面介绍一下符号扩展:将数据进行符号扩展是为了产生一个位数加倍、但数值大小不变的结果,以满足有些指令对操作数位数的要求,例如倍长于除数的被除数,再如将数据位数加长以减少计算过程中的误差。
以8位二进制为例,符号扩展就是指在保持值不变的前提下将其转换成为16位和32位的二进制数。
将0111 1111这个正的 8位二进制数转换成为 16位二进制数时,很容易就能够得出0000 0000 0111 1111这个正确的结果,但是像 1111 1111这样的补数来表示的数值,该如何处理?
直接将其表示成为1111 1111 1111 1111就可以了。
也就是说,不管正数还是补数表示的负数,只需要将 0 和 1 填充高位即可。
内存和磁盘的关系
我们大家知道,计算机的五大基础部件是 存储器、控制器、运算器、输入和输出设备,其中从存储功能的角度来看,可以把存储器分为内存和 磁盘,我们上面介绍过内存,下面就来介绍一下磁盘以及磁盘和内存的关系。
程序不读入内存就无法运行
计算机最主要的存储部件是内存和磁盘。
磁盘中存储的程序必须加载到内存中才能运行,在磁盘中保存的程序是无法直接运行的,这是因为负责解析和运行程序内容的 CPU 是需要通过程序计数器来指定内存地址从而读出程序指令的。
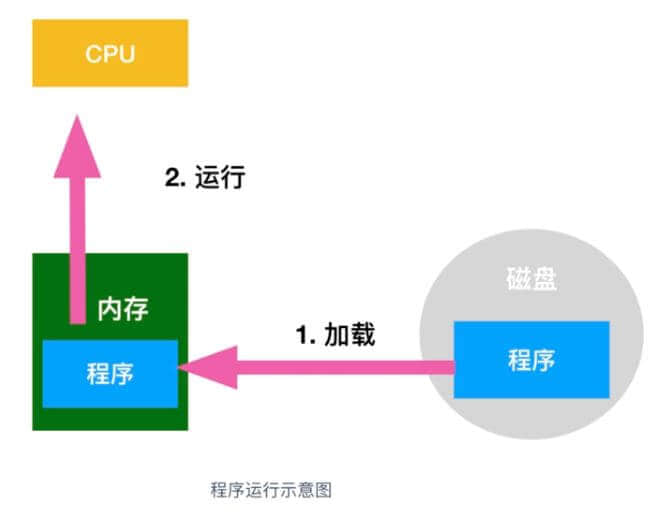
磁盘构造
磁盘缓存
我们上面提到,磁盘往往和内存是互利共生的关系,相互协作,彼此持有良好的合作关系。
每次内存都需要从磁盘中读取数据,必然会读到相同的内容,所以一定会有一个角色负责存储我们经常需要读到的内容。
我们大家做软件的时候经常会用到缓存技术,那么硬件层面也不例外,磁盘也有缓存,磁盘的缓存叫做磁盘缓存。
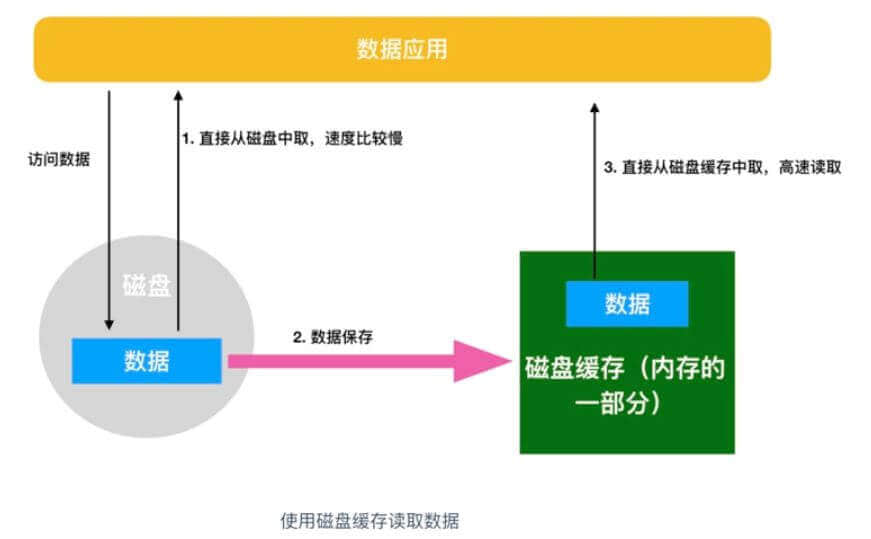
磁盘缓存指的是把从磁盘中读出的数据存储到内存的方式,这样一来,当接下来需要读取相同的内容时,就不会再通过实际的磁盘,而是通过磁盘缓存来读取。
某一种技术或者框架的出现势必要解决某种问题的,那么磁盘缓存就大大改善了磁盘访问的速度。
虚拟内存
虚拟内存是内存和磁盘交互的第二个媒介。
虚拟内存是指把磁盘的一部分作为假想内存来使用。
这与磁盘缓存是假想的磁盘(实际上是内存)相对,虚拟内存是假想的内存(实际上是磁盘)。
虚拟内存是计算机系统内存管理的一种技术。
它使得应用程序认为它拥有连续可用的内存(一个完整的地址空间),但是实际上,它通常被分割成多个物理碎片,还有部分存储在外部磁盘管理器上,必要时进行数据交换。
通过借助虚拟内存,在内存不足时仍然可以运行程序。
例如,在只剩 5MB 内存空间的情况下仍然可以运行 10MB 的程序。
由于 CPU 只能执行加载到内存中的程序,因此,虚拟内存的空间就需要和内存中的空间进行置换(swap),然后运行程序。
虚拟内存与内存的交换方式
虚拟内存的方法有分页式 和 分段式 两种。
Windows 采用的是分页式。
相关阅读 >>
更多相关阅读请进入《内存》频道 >>




